Այս համարում ընդգրված են հետևյալ նյութերը.

• Իմ ստեղծած հաշվիչը‎
• Երկրաչափական պատկերների գծումը scratch ծրագրով 
• Անդրադարձ ամսագրի նախորդ համարներին
• Խնդիր. «Քառակուսի և շրջան»
• Խաղ. «‎15»
• Խաղ. «‎Պենտամիմո»
• «Մոգական քառակուսի‎» ծագումը, լուծումը
• Խնդիրներ «‎Քվանտ» ամսագրից

Իմ ստեղծած հաշվիչը‎

Միջին դպրոցի սովորող՝ Ղազարյան Արտյոմը և Ղոչիկյան Տիգրանը ներկայացնում են scratch ծրագրով ստեղծած  էլեկտրոնային  հաշվիչների իրենց տարբերակները: Ղազարյան Արտյոմի աշխատանքը տե՛ս այստեղ, իսկ Ղոչիկյան Տիգրանի աշխատանքը՝ այստեղ: Հաշվիչը կատարում է միայն  պարզ թվաբանական գործողություններ:

 

 

 

 

 

 

Նյութի հեղինակ.
Ղազարյան Արտյոմ, Միջին դպրոց 7-րդ դասարան
Ղոչիկյան Տիգրան, Միջին դպրոց 7-րդ դասարան:

Երկրաչափական պատկերների գծումը scratch ծրագրով

Միջին դպրոցի սովորող Արտյոմ Ղազարյանը պատրաստել է ուսումնական նյութ scratch ծրագրով, ծրագիրը ցույց է տալիս, թե ինչպես գծել երկրաչափական պատկերներ՝ քառակուսի, հավասարակողմ եռանկյուն, շրջան և այլն: Գծելու համար անհրաժեշտ է ծրագրում մուտքագրել պատկերի կողմի երկարությունը: Աշխատանքը տե՛ս այստեղ:
Նյութի հեղինակ.
Ղազարյան Արտյոմ, Միջին դպրոց 7-րդ դասարան:

 

 

Անդրադարձ ամսագրի նախորդ համարներին

Միջին դպրոցի սովորողները անդրադարձել են ամսագրի  չորրորդ համարի հետևյալ նյութին՝ Ինչպե՞ս վանդակավոր թղթի վրա գծել շրջանագիծ՝ առանց կարկինի օգնության, աշխատանքը տե՛ս տեսանյութում.

Պատրաստեց՝ Հարությունյան Արեգ, Միջին դպրոց, 7-րդ դասարան:

Սովորողները նաև անդրադարձել են Ամսագրի  59-րդ համարի Քալլոթցի խնդրին:
Քալլոթցի խնդիրը (ամենապարզ, չլուծված խնդիրը):
Վերցրեք ցանկացած թիվ, եթե այն ​​զույգ է, ապա բաժանեք երկուսի: Եթե այն ​​կենտ է, բազմապատկեք երեքով և ավելացրեք մեկ: Կրկնեք գործողությունը: Արդյո՞ք բոլոր թվերն են, որ այդքան գործողություններից հետո արդյունքում միշտ կստացվի մեկ:
Ստուգենք խնդրի քայլերը օրինակ 9 թվի համար:
9×3+1=28
28:2=14
14:2=7
7×3+1=22
22:1=11
11×3+1=34
34:2=17
17×3=152
52:2=26
26:2=13
13×3+1=40
40:2=20
20:2=10
10:2=5
5×3+1=16
16:2:2:2:2=1, ստացանք մեկ: Տարբեր թվերի համար նույն խնդիրը փորձարկել են հետևյալ սովորողները՝

Արգիշտի Ղարիբյան
Դավիթ Մկրտչյան
Դավիթ Մուրադյան
Աննա Թադևոսյան
Գաբրիելյան Վահե
Հարությունյան Արեգ

Խնդիր. «Քառակուսի և շրջան»

Վերցրեք հաստ թուղթ և նրա վրա կտրեք 8 սանտիմետր կողմով քառակուսի, տե՛ս նկարը:

Այնուհետև ստվարաթղթից կտրեք 7,5 սմ շառավղով շրջան, տե՛ս նկարը։(Ավելի համար է վերցնել ոչ շատ հաստ ստվարաթուղթ, լավագույն հաստությունը՝ 2մմ-3մմ):

Խնդիրը հետևյալն է. ինչպես ստվարաթղթե շրջանը անցկացնել  քառակուսաձև անցքի միջով, առանց  շրջանի ձևափոխման, այսինքն, չի թույլատրվում շրջանը ճկել, ծալել,կտրել և այլն, իսկ քառակուսի անցքով թուղթը կարելի է:
Հարց: Ի՞նչ առավելագույն տրամագիծ պետք է ունենա շրջանը, որ կարողանա անցնի քառակուսաձև անցքով։

Աղբյուրը՝ «‎Քվանտ» ամսագիր, էջ՝ 2:
Նյութը իրարից անկախ թարգմանեցին՝
Թադևոսյան Ալեքսանդրը, Գաբրելիայն Վահեն, Մուրադյան Դավիթը, Հարությունյան Արեգը, Միջին դպրոց, 7-րդ դասարան:

Իաղ. «‎15»

Այս խաղը, եթե փորձենք հակիրճ ներկայացնել, ապա այն  նույն Ռուբիկ -Կուբիկ խաղն է, պարզապես ոչ թե եռաչափ տարածությունում 3x3x3, այլ՝ երկչափ 4×4:
Դիցուք ունենք  4×4 հիմքով տուփ, որում տեղավորված են 1×1 չափով սալիկներ, բոլոր սալիկները  համարակալված են 1-16 թվերով: Տուփից հանենք 16 համարի սալիկը, կմնա 15 սալիկ: Հանելուց հետ, բնականաբար  տուփում մեկ  1×1 սալիկի  ազատ տեղ կմնա, ինչի շնորհիվ կարելի է ազատ տեղաշարժել հարևան սալիկները, տես նկարը:

Ազատված տեղում նորից կարելի է տեղափոխել հարևան սալիկներից մեկը և այդպես շարունակ։ Պահանջվում է սալիկների կամայական ձևով դասավորված տուփում սալիկները տեղափոխելով դասավորել ըստ համարների հերթականության։
Այս խաղը ստեղծվել է ԱՄՆ-ում, XIX դարի երկրորդ կեսին:
Թարգմանեց՝  Աննա Թադևոսյան, Միջին դպրոց, 7-րդ դասարան:
Աղբյուրը՝ «‎Քվանտ» ամսագիր, էջ 16:

Խաղ. «‎Պենտամիմո»

Պոլիմինոն երկչափական պատկերներ են, որոնք կազմված են միավոր քառակուսիներից, և կախված քառակուսիների թվից դրանք ստացել են առանձին անվանումներ, ինչպես օրինակ՝

• Մոնիմինո
• Դոմինո
• Տրիմինո
• Տետրամինո
• Պենտամինո
• Հեքսամինո
• Հեպտամինո
• Օկտամինո
• Նոնամինո
• Դեկտամինո և այլն…

Պոլիմինոն, որը կազմված է հինգ միավոր քառակուսիներից և ծածկում է շախմատի տախտակի հինգ վանդակները, ստացել է պենտամինո անվանումը: Գոյություն ունի 12 պենտամինո: Տե՛ս նկարում.

Պենտամինոյի ամենատարածված խնդիրներից մեկն է դասավորել բոլոր 12 պատկերները մեկ ուղղանկյան մեջ այնպես, որ որևէ բաց վանդակ չմնա և, քանի որ յուրաքանչյուր պենտամինո կազմված է 5 քառակուսիներից, ապա այդ ուղղանկյունը պետք է պարունակի 5×12=60 միավոր քառակուսի: Այդպիսի հնարավոր ուղղանկյուններ են  ՝ 6×10; 5×12; 4×15 և 3×20 ուղղանկյունները:

6×10 ուղղանկյան դեպքում խնդիրն առաջինը լուծել է Ջ. Ֆլեչերը 1965 թվականին:
Այս դեպքի համար գոյություն ունեն 2339 տարբեր լուծումներ:
5×12 ուղղանկյան համար լուծումները 1010-ն են, 4×15-ի դեպքում՝  368, իսկ 3×20-ն ունի ընդամենը 2 լուծում:

Աղբյուրը՝ դասավանդող  Լուսինե Ներսեսյանի բլոգ:

«Մոգական քառակուսի»  ծագումը, լուծումը‎

 Մոգական քառակուսին 1-ից մինչև nxn թվերի հաջորդականություն է, որոնք դասավորված են nxn քառակուսու վանդակներում այնպես, որ բոլոր տողերի, սյուների, երկու անկյունագծերի թվերի գումարը լինի նույնը:
Մոգական քառակուսիների  մասին առաջին հիշատակումները եղել են հին չինացիների կողմից: Ըստ լեգենդի՝ Յու կայսրի օրոք (մ.թ.ա. մոտ 2200 թ.) Դեղին գետի ջրերից դուրս է եկել մի սուրբ կրիա, որի պատյանի վրա գրված են եղել խորհրդավոր հիերոգլիֆներ, տես նկարը, հաշվելով կրիայի պատյանի վրա յուրաքանչյուր պատկերում նշված կետերի քանակը, ստացել են մոգական քառակուսի:

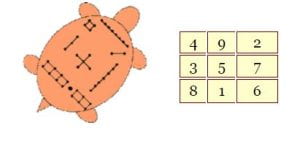
Հազվադեպ է պատահում, որ մոգական քառակուսիները  օգտագործվեն կերպարվեստում: Առաջին անգամ օգտագործել է  գերմանացի նկարիչ Ալբրեխտ Դյուրերը (1471 – 1528), ով 1514 թվականին թողարկեց «Մելանխոլիա» փորագրությունը, որում առկա է 4×4 մոգական քառակուսի։ Ավելին, նկարի ներքևի տողի երկու թվերը ցույց են տալիս փորագրության ստեղծման տարեթիվը` 1514: Ասում են, որ Ա.Դյուրերի փորագրությունը խթան է ծառայել իր ժամանակակից Միշել Նոստրադամուսի (1503-1566) հայտնի մարգարեությունների համար։

3×3 Մոգական  քառակուսու լուծումը:

3×3 մոգական  քառակուսու մեջ մոգական հաստատունը 15-ն է` (1+2+3+4+5+6+7+8+9):3=15, որը  պետք է հավասար լինի ութ ուղղություններով երեք թվերի գումարին՝ 3 տող, 3 սյունակ և 2 անկյունագիծ: Քանի որ կենտրոնում գտնվող թիվը պատկանում է 1 տողին, 1 սյանը,  2 անկյունագծին, այն ներառված է 8 եռյակներից 4-ում, որոնք գումարվում են մոգական հաստատունին, ապա այդ թիվը միայն 5 է։ Հետևաբար, 3×3 մոգական քառակուսու կենտրոնում գտնվող թիվն արդեն հայտնի է՝ այն հավասար է 5-ի։Դիտարկենք 9 թիվը։ Այն ներառված է թվերի միայն երկու եռյակի մեջ։ Մենք չենք կարող այն տեղադրել անկյունում, քանի որ յուրաքանչյուր անկյունային վանդակ  պատկանում է 3 եռակի՝ տող, սյունակ և անկյունագիծ: Հետևաբար, 9 թիվը պետք է լինի մեջտեղի քառակուսու կողմին հարող մի վանդակում: Քառակուսու համաչափության պատճառով կարևոր չէ, թե որ կողմն ենք ընտրում, ուստի կենտրոնական վանդակում 5 թվից վեր գրում ենք 9: Վերևի գծի 9-ի երկու կողմերում մենք կարող ենք մուտքագրել միայն 2 և 4 թվերը: Այս երկու թվերից ո՞րը կլինի վերևի աջ անկյունում, իսկ որը՝ ձախում, դարձյալ նշանակություն չունի, իսկ մնացած վանդակները լրացվում են ավտոմատ կերպով: 

Ստորև ներկայացված է 3×3 մոգական քառակուսու  օրինակ:

Աղբյուրը` դասավանդող Սյուզի Հակոբյանի բլոգ:

Խնդիրներ «‎Քվանտ» ամսագրից

1.Վանյան իրարից տարբեր թվանշանները դասավորեց եռանկյան գագաթներում պատկերված շրջաններում և եռանկյունների  ներսում գրեց  այդ եռանկյան գագաթներում գրված թվերի գումարը կամ արտադրյալը, հետո թվանշանները ջնջեց, տես նկարը: Գտեք  շրջաններում  գրված թվանշանները:

2. Երեք գորտ հերթականությամբ թռան ճահճից: Յուրաքանչյուրը թռավ այնպես, որ ընկավ մյուս երկուսի միջև ընկած հատվածի մեջտեղում: Երկրորդ գորտ ցատկի երկարությունը 60սմ: Գտե՛ք երրորդ գորտի ցատկի երկարությունը:

3. 0-ից 9 թվանշանները ինչ-որ հերթականությամբ ծածկագրված են հետևալ տառերով՝
A, B, C, D, E, F, G, H, I, J: Մեկ հարցով  կարելի է իմանալ ծածկագրված գումարի իրարից տարբեր տառերը։
Օրինակ, եթե հարցնենք, ինչի է հավասար «A + B» -ն, ընդ որում՝  A -9, B- 1, C-0, ապա  պատասխանը կլինի «A ​​+ B = BC»: Ինչպե՞ս կարելի  հինգ  հարցով  որոշել, թե ո՞ր տառերը ո՞ր թվանշաններին են համապատասխանում:

4. ABCD քառանկյան մեջ հայտնի, որ AB =BC= CD, <A =70 աստիճան, իսկ
<B= 100 աստիճան: Գտեք  անկյուն C  և անկյուն D-ի աստիճանային չափերը:

 

Թարգմանեց Անժելիկա Մնացականյանը, Միջին դպրոց, 7-րդ դասարան:
Խնդիրներ «‎Քվանտ» ամսագրից էջ՝ 30: