Այս համարում ներառված են հետևյալ նյութերը՝

1. Սեղանի խաղ-գլուխկոտրուկ
2. Ճանաչեք մաթեմատիկոսներին
3. Մաթեմատիկական խաղ-խաչբառ
4. Պարզ թվեր, կիրառությունը
5. Լեոնարդ Էյլեր. «Քյոնիգսբերգի յոթ կամուրջները»
6. Գիտես, որ…
7. Խնդիրների թարգմանություն «Քվանտ» ամսագրից

 

1. Սեղանի խաղ-գլուխկոտրուկ

Ձեզ ենք ներկայացնում  կանադացի գյուտարար Ֆրեդերիկ Բուշեի սեղանի խաղ- գլուխկոտրուկը: Այն բաղկացած է յոթ դետալներից, տե՛ս նկարը, որոնցից յուրաքանչյուրը ներկայացնում է   2 x 1 x 1  չափերով  2 իրար սոսնձված ուղղանկյունանիստեր:

Սա տարածական  գլուխկոտրուկներից թերևս ամենահայտնին է: Խաղի դետալները կարծես Տետրամինո խաղի տարածական մարմինները լինեն:

Խաղը կայանում է հետևյալում.Փորձեք վերը նկարագրված յոթ դետալները դասավորել  4x4x2 տուփում:

Տուփի ծավալը  32 է, իսկ բոլոր դետալների  ընդհանուր ծավալը 28 է, այնպես որ, կարող է թվալ, որ տուփում ավելորդ տեղ կա և դետալները  հեշտությամբ կտեղավորվեն տուփի մեջ:Ամեն դեպքում, հիմնական դժվարությունը կայանում է նրանում, թե ինչպես ճիշտ դասավորել  ոչ ստանդարտ տետրիմինները՝ դետալները,  որ տուփից նրանք  դուրս չգան,  եթե հասկացել եք ձևը, ապա գլուխկոտրուկն արագ կլուծվի:
Դե ինչ, մաղթում ենք հաջողություն:

Նյութը ներկայացրեց  Իռեն Կարապետյանը, Միջին դպրոց, 8-րդ դասարան:
Խաղի աղբյուրը տե՛ս այստեղ, էջ1:

 

2. Ճանաչեք  մաթեմատիկոսներին

Հյուսիսային դպրոցի մաթեմատիկա դասավանդող Անի Միրզոյանն և ընեկները առաջարկում են՝ ճանաչեք մեծ մաթեմատիկոսներին շարքը .

Վիկտոր Համբարձումյան, տեսանյութը ստորև՝

Արքիմեդես՝ ռադիոնյութը  այստեղ:

Լեգենդները պատմում են, որ Արքիմեդեսը հաճախ մոռանում էր ուտելու մասին, երկար ժամանակ չէր լողանում և ամենուրեք պատրաստ էր գծագրել. փոշու մեջ, ավազի վրա, մոխրի մեջ, նույնիսկ իր սեփական մարմնի վրա։ Մի անգամ լողանալու ժամանակ նրա մոտ հանկարծ միտք է ծագում այն հրող ուժի մասին, որը դուրս է մղում մարմինը հեղուկի միջից և, մոռանալով ամեն ինչի մասին, մերկ, վազում է Սիրակուզայի փողոցով հաղթական աղաղակով՝ «Էվրիկա», «Էվրիկա»,   Ես գտա․․․

3. Մաթեմատիկական խաղ-խաչբառ

Միջին դպրոցի սովորող Գուրգեն Մանուկյանը ներկայացնում է իր  պատրաստած  մաթեմատիկական խաղ –խաչբառը, խորհրդատու՝  Արշակ Մարտիրոսյան, Միջին դպրոցի մաթեմատիկայի դասավանդող:

Հարցերը տե՛ս այստեղ:

 

4. Պարզ  թվեր, կիրառությունը (մաս 2)

Պարզ թվերի, տեսակների  մասին ներկայացրել ենք  նախորդ համարում։Այս համարում կխոսենք նրանց կիրառելության մասին:

Հիշեցնենք, որ մաթեմատիկայում պարզ թվերը բնական թվեր են, որոնք ունեն միայն երկու բաժանարար, բաժանվում են միայն մեկի և իրենց վրա:  1-ը չի համարվում ոչ պարզ, ոչ բաղադրյալ թիվ։ Առաջին քսան բնական թվերի շարքում պարզ են հետևալ թվերը՝

P₁= 2
P₂= 3
P₃= 5
P₄= 7
P₅= 11
P₆= 13
P₇= 17
P₈= 19

մնացածը, բացի 1-ից, բաղադրյալ են։ Պարզ թվերը նման են անտրոհելի տարրերի, որոնցով բազմապատկման գործողության միջոցով կարելի է ստանալ բոլոր բնական թվերը։ Դա նման է ֆիզիկայում  տարրական մասնիկների դերին կամ նրան, որ բոլոր քիմիական նյութերը կարելի է սինթեզել Մենդելեևի քիմիական տարրերի պարբերական աղյուսակի տարրերից։ Պարզ թվերի նման դերակատարումն այնքան է կարևորվել, որ համապատասխան պնդումը, ավելի ճիշտ՝ բնական թվերի՝ պարզ թվերի արտադրյալի տեսքով ներկայացման հնարավորության (այսինքն՝ գոյության) և միակության մասին պնդումը, ստացել է «Թվաբանության հիմնական թեորեմ» անվանումը։  Մաթեմատիկայում և այլուր պարզ թվերը հանդիպում են ամենատարբեր իրադրություններում։ Գիտակների համար հիշատակենք, որ պարզ թվերի հետ են առնչվում, օրինակ, դաշտերի բնութագրիչները, ոչ արքիմեդյան նորմավորումները, SpecZ֊-ի կետերը և այլն։
Ինչպես նշել է թվերի տեսության հայտնի մասնագետ Ա. Խինչինը. «Պարզ թվերի հիմնարար դերը  բևեռել է  հետազոտողների ուշադրությունը։ Ինչպիսին է նրանց բազմությունը, քանի թիվ է պարունակում, ինչպես են նրանք
բաշխված, ինչպիսի օրինաչափությունների են ենթարկվում պարզ և բաղադրյալ թվերի իրար հաջորդումը բնական թվերի շարքում» և այլն։ Բոլոր այս հարցերը բնականորեն կանգնել են տարբեր դարաշրջանների գիտնականների առջև՝ սկսած անտիկ աշխարհից մինչև մեր օրերը, և  այժմ էլ զգալի չափով գտնվում են թվաբանական գիտության ուշադրության կենտրոնում, հատկապես այն պատճառով, որ նրանց գտնելը մեծ դժվարություն է առաջացնում։
Գոյություն ունի հին հույներից ավանդված մի պարզ և գեղեցիկ եղանակ՝  պարզ թվերը ստանալու համար, որը կոչվում է էրատոսթենեսի մաղ՝ այն առաջինը կիրառած հին հույն մաթեմատիկոս էրատոսթենեսի պատվին։

Տանք հակիրճ տեղեկություններ նրա մասին։ Համարվում է, որ էրատոսթենեսը ապրել է մեր թվարկությունից առաջ 276 — 194 թթ.։ Ծնվել է Հյուսիսային Աֆրիկայի Կիրենա քաղաքում, որը գտնվում է ժամանակակից Լիբիայում, սովորել և կյանքի մեծ մասն անցկացրել է Եգիպտոսի Ալեքսանդրիա քաղաքում, նրա հռչակավոր գրադարանում։
էրատոսթենեսի բազմակողմանի գիտելիքները բարձր է գնահատել նրա ժամանակակից և ավագ գործընկեր Արքիմեդը։

էրատոսթենեսի մաղի մեթոդը կիրառվում է հետևյալ կերպ։ Գրենք աճման կարգով  բնական թվերը՝ սկսած երկուսից մինչև որևիցե ո բնական թիվ։ Ապա «մաղենք» այդ թվերը։ Նախ ջնջենք (կամ ընդգծենք, կամ ներկենք այլ գույնի) բոլոր այն թվերը, որոնք բաժանվում են երկուսի՝ բացի հենց երկուսից. երկուսից հետո հաջորդ թիվը կլինի երեքը։ Թողնելով այն՝ ջնջենք բոլոր երեքի բաժանվող թվերը։ Եվ այդպես վարվենք շարւնակ, հերթական ջնջումից հետո առաջին չջնջված թիվը թողնենք, իսկ նրան բաժանվող բոլոր մնացած թվերը ջնջենք։ Գրված թվերն այսպես «մաղելուց» հետո կմնան միայն պարզ բնական թվերը, իսկ բոլոր բաղադրյալ թվերը «կմաղվեն»։ Օրինակ՝ ո = 100 դեպքում կունենանք հետևյալ պատկերը.

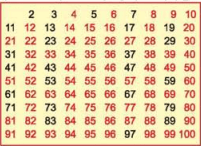
Համաձայն այս աղյուսակի, 15-րդ պարզ թիվը կլինի՝
P₁₅= 47
P₂₅ = 97։

Մեծացնելով ո-ը՝ կարելի է գտնել նոր մեծամեծ պարզ թվեր։ Օրինակ՝
P₃₅ = 149
P₄₆= 199
P₇₀ = 349
P₉₅ = 499
P₁₀₀ = 541
P₂₀₀ = 1223
P₃₀₃ = 1999։
(Այսպիսով՝ անցյալ դարի վերջին տարեթիվը պարզ թիվ է եղել:
Հարց է առաջանում. Քանի՞ պարզ տարեթիվ կլինի երրորդ հազարամյակի առաջին դարում):
Մինչև 1950 թ. հայտնի ամենամեծ պարզ թիվը եղել է 2^127 -1 թիվը, որն ունի 39 տասնորդական թվանշան, ընդ որում, այդ թվի պարզ լինելը դեռ 1876 թ. ապացուցել է ֆրանսիացի մաթեմատիկոս Լյուկան։ 1909 թ. հրատարակվել են 10 միլիոնից փոքր բոլոր պարզ թվերի աղյուսակները։ 1951 թ. այդ աղյուսակները լրացվել են և գտել են  10.999.997  փոքր բոլոր պարզ թվերը,  իսկ 1959 թ. կազմվել է P_6000000 = 104395301 պարզ թիվը չգերազանցող բոլոր պարզ թվերը պարունակող միկրոֆիլմ։ 1963 թ. հայտնի ամենամեծ պարզ թիվը 2 ^4423 -1 էր, որն ունի 1332 թվանշան։ Ապացուցված է, որ գոյություն ունեն առնվազն երեք պարզ թվեր, որոնց թվանշանների քանակը հավասար է 1000, սակայն ոչ մի այդպիսի թիվ հայտնի չի եղել գոնե մինչև 1963 թ.։

Ցանկացած նոր պարզ թվի հայտնաբերումը համարվում է մեծ առաջընթաց։ Համակարգիչների ստեղծումից հետո սկսվում է ռեկորդների մրցավազք՝ նոր
մեծ պարզ թվեր գտնելու համար։ Եթե մինչև 1951 թ., ինչպես վերը
ասացինք, ամենամեծ հայտնի պարզ թիվը 39 նիշ ունեցող 2^ 127–1
թիվն էր, ապա դրանից հետո տեղի է ունենում իսկական պոռթկում։ 1951 թ. մինչև 1971 թ. հայտնաբերվում են 15 նոր պարզ թվեր։ Թե նրանց հայտնաբերումն ինչ հետաքրքրություն է առաջացնում հասարակության շրջանում, վկայում է, օրինակ, հերթական նորահայտ պարզ թվին նվիրված ամերիկյան փոստային շտամպը (կնիքը), որի վրա տպված էր 2^11213 — 1 » ( 2¹¹²¹³ -1 թիվը պարզ է) արձանագրությունը և այդ 3 376 տասնորդական նիշ ունեցող թիվը։ Երբ 1978 թ. Կալիֆոռնիայից երկու դպրոցականներ  սահմանում են նոր ռեկորդ՝ մատնանշելով, որ  2^21701 -1 պարզ թիվ է: Մի գերմանական թերթ գրում է. «էրատոսթենեսի մաղով հաջողվել է որսալ ամենամեծ պարզ թիվը»։ Այս առիթով մասնագետներից մեկը հումորով նկատում է, որ էրատոսթենեսի մաղը դրա համար պիտանի է նույնքան, որքան կացինը՝ ատոմի միջուկը ճեղքելու համար։

Շատ չանցած վերոհիշյալ արդյունքը գերազանցվում է, նախ ապացուցվում է, որ պարզ են 2^23209 –1, ապա 2^44497 -1 թվերը։ 1983 թ. հայտարարվում է, որ պարզ է 25962 թվանշանից կազմված 2^86243 -1 թիվը։ Թե ինչ արագությամբ են տեղի ունենում փոփոխությունները, վկայում են հետևյալը։ Ամերիկյան մաթեմատիկական ընկերության հեղինակավոր «Nottices of the AMS» ամսագրի 2004 թ. ապրիլյան համարում «The Great Prime Number Record Races» («Մեծ պարզ թվի ռեկորդ է գրանցվել») հոդվածում որպես նորահայտ մեծագույն պարզ թիվ՝ նշվում է
6 320 430 տասնորդական թվանշան ունեցող 2^20996011 -1 թիվը, իսկ նույն ընկերության հուլիսի կեսերի Website֊ում (կայքում) տեսնում ենք, որ ամենամեծն արդեն
2^24036583 — 1 պարզ թիվն է, որն ունի ավելի քան յոթ միլիոն տասնորդական թվանշան։ Նշվում է նաև, որ 100 000 դոլար մրցանակ է սահմանվել 10 միլիոն թվանշանից կազմված պարզ թիվ հայտնաբերողին ։
Ստորև բերվող աղյուսակում գրանցված են առ 2008 թվականի սեպտեմբեր ամիսը հայտնի ամենամեծ պարզ թվերը։ Առաջին սյունում համարակալվում է նրանց հաջորդականությունը նվազման կարգով, երկրորդում նշված են այդ թվերը, երրորդում՝ նրանց տասնորդական թվանշանների քանակը, չորրորդում՝ նրանց հայտնաբերման տարեթիվը։

Սույն հոդվածը տպագրության հանձնելուց հետո Ամերիկյան մաթեմատիկակ ան Միության 2008 թ. հոկտ եմբեր ամսի կայքում հայտարարություն եղավ, որ հայտնաբերվել են 13 միլիոն թվանշան ունեցող Մերսենի 45֊-րդ՝ 2^43112609 — 1 պարզ թիվը և ապա 11 միլիոն թվանշանից կազմված Մերսենի 46-րդ՝ 2^ 37156667-1 պարզ թիվը։ Հայտնաբերողներից յուրաքանչյուրը ստացել է 50 հազար դոլար մրցանակ ։ Նոր՝ 150 հազար դոլար, մրցանակ է հայտարավել 100  միլիոն կամ ավելի նիշ ունեցող առաջին պարզ թիվը հայտնաբերողին։

Ինչպես տեսնում ենք, 150 000 դոլար մրցանակը դեռ  սպասում է իր տիրոջը։

Նյութի աղբյուրը՝ Թաթուլ Շահնազարյանի բլոգ, Ավագ դպրոց, մաթեմատիկա դասավանդող:

 

5. Լեոնարդ Էյլերը . «Քյոնիգսբերգի յոթ կամուրջները»

Լեոնարդ Էյլերը ծնվել է 1707 թվականի ապրիլի 15-ին  Շվեյցարիայի Բազել քաղաքում  և մահացել է Սանկտ Պետերբուրգում, 1783 թվականի նոյեմբերի 18-ին:
Լեոնարդը նախնական կրթություն ստացել է  տանը ՝ հոր ղեկավարությամբ, ով իր ժամանակ մաթեմատիկա էր սովորել Յակոբի Բեռնուլիի մոտ և  նշանակալի նվաճումներ է ունեցել որպես մաթեմատիկոս։Էյլերն իր հիմնական կրթությունը ստացել է Բազելի գիմնազիայում, որտեղ նա ապրում էր իր մորական տատիկի հետ (շարունակելով միաժամանակ խորությամբ ուսումնասիրել մաթեմատիկան): 1720 թվականին, տասներեք տարեկանում, նա հնարավորություն է ունեցել Բազելի համալսարանում մասնակցել դասերի, որտեղ նա գրավում է Իոհան Բեռնուլիի (Յակոբի Բեռնուլիի փոքր եղբոր) ուշադրությունը։ Ճանաչված գիտնականը, ուսումնասիրման համար, Էյլերին է փոխանցում մաթեմատիկական հոդվածներ, թույլատրելով անհասկանալի հարցերի պարզաբանման համար այցելել իրեն շաբաթ օրերին՝ ճաշից հետո։

1720 թվականի հոկտեմբերի 20-ին, 13-ամյա Լեոնարդ Էյլերը դարձավ Բազելի համալսարանի մշակույթի ֆակուլտետի ուսանող։ Այցելելով իր ուսուցչին, Լեոնարդը ծանոթացավ և սկսեց ընկերություն անել նրա որդիների՝ Դանիել Բեռնուլիի և Նիկոլայ Բեռնուլիի հետ, որոնք նույնպես, ընտանեկան ավանդույթի համաձայն, խորապես ուսումնասիրում էին մաթեմատիկան։ 1723 թվականին Էյլերը, Բազելի համալսարանում ստացավ իր առաջին մրցանակը:1741 թվականին Ֆրիդրիխ Մեծի խնդրանքով, ավելի ճիշտ ՝ հրամանով, նա տեղափոխվեց Բեռլին, որտեղ նա  դարձավ գիտությունների ակադեմիայի անդամ և մաթեմատիկայի պրոֆեսոր: Նա հարստացրեց Բեռլինի  «Melanges» կամ «Miscellanies» – ի վերջին հատորը հինգ հուշագրություններով, դրանից հետո զարմանալի արագությամբ հաջորդեցին մեծ թվով կարևոր հետազոտություններ։
Հենց այդ ժամանակաշրջանն էր, որ նա իր ամբողջ  գիտելիքը  հասցրեց կատարելության, ավելի բարձր աստիճանի, հայտնագործեց սինուսների հաշվարկը, վերլուծական գործողությունները իջեցնելով ավելի  պարզության և նոր լույս սփռեց  մաթեմատիկայի գրեթե բոլոր ճյուղերի  վրա:

1735 թ.-ին Ակադեմիայի կողմից առաջարկված աստղագիտական ​​խնդիրը, որի լուծման համար մի քանի ականավոր մաթեմատիկոսներ պահանջել էին մի քանի ամիս ժամանակ, Լեոնհարդ էյլերը լուծեց երեք օրվա ընթացքում `իր իսկ կատարելագործված մեթոդների օգնությամբ, բայց  այդ ջանքերից նա հիվանդացավ  և զրկվեց  աջ աչքից:
Էյլերի աշխատաքնները, իհարկե  շատ  են ու մեկը մյուսից հետաքրքիր և բովանդակալից, սակայն այս անգամ մենք կուսումնասիրենք հետևյալ խնդիրը՝ «Քյոնիգսբերգի յոթ կամուրջները»,  որի լուծումը  առաջարկել է Էյլերը։

 

«Քյոնիգսբերգի յոթ կամուրջները»

«Քյոնիգսբերգի յոթ կամուրջները» մաթեմատիկական հին  խնդիր է: 1735 թվականին  Լեոնարդ Էյլերի լուծումը հիմք դրեց գրաֆների տեսությանը:

Պրուսիայի Քյոնիգսբերգ քաղաքը գտնվում էր Պրեգոլյա գետի երկու ափերին։ Քաղաքը բաժանված էր չորս ցամաքների, որոնք կապված էին միմյանց  յոթ կամուրջներով։
Խնդիրը հետևյալն էր. Անցնել ողջ քաղաքը` օգտագործելով բոլոր յոթ կամուրջները, ընդ որում յուրաքանչյուր կամրջով կարելի էր անցնել միայն մեկ անգամ։ Չէր կարելի օգտագործել որևէ այլ ճանապարհ, բացի կամուրջներից։ Բացի այդ չէր թույլատրվում կամրջի կեսից ետ դառնալ։ Շրջագայությունը կարող էր ավարտվել սկզբնակետից բացի ցանկացած այլ կետում։

Էյլերն ապացուցեց, որ խնդիրը  լուծում չունի, ինչի արդյունքում էլ ծնվեց ժամանակակից գրաֆների տեսությունը:

Էյլերը նկատեց, որ ճանապարհի ընտրությունը խնդրի լուծման համար կարևոր չէ։ Կարևորը՝ կամուրջներով անցնելու հերթականությունն է։ Սա հնարավորություն տվեց նրան վերակազմել խնդիրը աբստրակտ պայմաններով։ Նա հեռացրեց ամեն ինչ, բացի ցամաքային տարածքներից և դրանք կապող կամուրջներից։ Էյլերը ցամաքային մասերը փոխարինեց կետերով՝ A, B, C, D, իսկ կամուրջները՝ գծերով։ Յուրաքանչյուր գիծ՝ կամուրջ (օրինակ՝AB) ցույց էր տալիս, թե որ գագաթը (ցամաք) որին էր միացված։ Այսպես նա ստացավ գրաֆ: Այսպիսով, նա այժմ կարող էր նկարագրել կամրջի միջով անցումը A տարածքից մինչև B տարածք, որպես AB ճանապարհ, իսկ ճանապարհը A տարածքից B տարածքով դեպի տարածք D` որպես ABD:

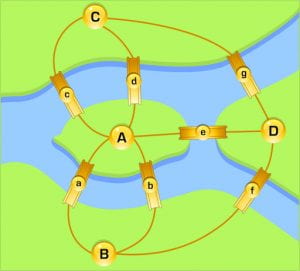
Այստեղ կարևոր է նշել, որ երթուղու նկարագրության տառերի քանակը միշտ կլինի մեկով ավելի, քան հատված կամուրջների քանակը: Այսպիսով, AB երթուղին անցնում է մեկ կամրջով, իսկ ABD երթուղին անցնում է երկու կամրջով  և այլն: Էյլերը հասկացավ, որ քանի որ Կոնիգսբերգում կա յոթ կամուրջ և բոլորն անցնելու համար երթուղին պետք է բաղկացած լինի ութ տառից, ինչը նշանակում է, որ խնդրի լուծման համար անհրաժեշտ կլինի ուղիղ ութ տառ:
Հետո նա այն բերեց ավելի ընդհանուր սխեմայի։
Եթե ​​դուք ունենայիք միայն երկու ցամաքային հատվածներ ՝ A և B  և մեկ անգամ կապող կամուրջ, ապա A ցամաքը կարող էր լինել այն տեղը, որտեղ ճանապարհորդությունը սկսվեց կամ այն տեղը  որտեղ ավարտվեց, բայց դուք միայն մեկ անգամ կլինեիք A հատվածում:  Եթե ​​մեկ անգամ անցնեք A, B և C կամուրջները, ապա ուղիղ երկու անգամ կհայտնվեիք A հատվածում: Սա հանգեցրեց մի կանոնի.

Եթե ցամաք տանող կամուրջներ ունեք, ապա այդ թվին պետք է ավելացնեք մեկը, ապա ընդհանուրը բաժանեք երկուսի վրա ՝ պարզելու համար, թե քանի անգամ է այդ հատվածը օգտագործելու ձեր ճանապարհորդության ընթացքում:
Այս արդյունքը բերեց էյլերին հետևյալ  խնդրին:

Խնդիր: Կան հինգ կամուրջ, որոնք տանում են դեպի  A, ուստի նրա որոնած ութ տառանոց լուծումը պետք է հատվի երեք անգամ՝ B, C և D հատվածներն ունեն երկու կամուրջ, որոնք տանում են դեպի իրենց, ուստի յուրաքանչյուրը պետք է երկու անգամ անցնի: Բայց 3 + 2 + 2 + 2-ը 9-ն է, ոչ թե 8-ը, չնայած ըստ պայմանի `պետք է անցնել ընդամենը 8 հատվածով և անցնել 7 կամուրջ: Սա նշանակում է, որ անհնար է անցնել Կոնիգսբերգ քաղաքով մեկ ՝ օգտագործելով յուրաքանչյուր կամուրջ ուղիղ մեկ անգամ: Այլ կերպ ասած, այս դեպքում խնդիրը լուծում չունի ։
Այլ կերպ ասած, մուտքերի և ելքերի քանակը պետք է հավասար լիներ։ Հետևաբար, բացի սկզբնական և վերջնական գագաթներից` յուրաքանչյուր գագաթին կից կամուրջների թիվը պետք է զույգ լինեն։ Այնուամենայնիվ, բոլոր գագաթների աստիճանները կենտ էին. մեկից դուրս էր գալիս հինգ կամուրջ, իսկ մյուսներից՝ երեքական։

Գրաֆների տեսության մեջ գրաֆի բոլոր կողերը մեկ անգամ այցելող ուղին կոչվում է Էյլերյան զբոսանք՝ ի պատիվ Էյլերի։ Պարզվում է, որ կապակցված գրաֆում Էլյերյան փակ զբոսանքի գոյության համար անհրաժեշտ է և բավարար, որ բոլոր գագաթներն ունենան զույգ աստիճաններ։ Էյլերի լուծման հանճարեղիությունը նույնիսկ պատասխանի մեջ չէ, այլ նրա կիրառած մեթոդի: Դա գրաֆիկի տեսության ամենավաղ օգտագործման դեպքերից մեկն էր, որը հայտնի է նաև որպես ցանցի տեսություն, մաթեմատիկայի խիստ փնտրված ոլորտը այսօրվա աշխարհում ՝ լցված տրանսպորտային, սոցիալական և էլեկտրոնային ցանցերով: Ինչ վերաբերում է Կյոնիգսբերգին, ապա քաղաքն ի վերջո ստացավ ևս մեկ կամուրջ, որը վիճահարույց դարձրեց Էյլերի որոշումը, իսկ այնուհետև Երկրորդ համաշխարհային պատերազմի ժամանակ բրիտանական ուժերը ավերեցին քաղաքի մեծ մասը:Այնուամնեայնիվ,  այսօր թե՛ քաղաքը, թե՛ գետը ունեն նոր անուններ ունեն:, բայց հին խնդիրն ապրում է մաթեմատիկայի բոլորովին նոր ոլորտում:

Խնդիր: Փորձեք նկարել  բոլոր  այս պատկենրերը հետևյալ կանոնով.

• նկարել առանց  ձեռքը թղթից հանելու
• յուրաքանչյուր կողմով անցնելով միայն մեկ անգամ:

 

 

 

 

 

Նյութի հղումը 1, 2, 3:

Նյութը պատրաստեց  Միջին դպրոցի մաթեմատիկայի դասավանդող Սյուզի Հակոբյանը:

 

6. Գիտե՞ս, որ…

Գիտես, որ … շարքը ներկայացնում է Զարինե Փանյանը, Միջին դպրոցի դասավանդող:

1․Սահմանում: Պալինդրոմ են կոչվում այն թվերը, որոնք աջից և ձախից կարդալիս ստացվոմ են նույն թիվը։
Օրինակ՝ 143341 , 8558, 222 և այլն։ Գիտե՞ս, որ բոլոր քառանիշ պալինդրոմ թվերը բաժանվում են 11-ի։
Օրինակ՝ 7227 ։ 11 = 657,  իսկ թե ինչու են այդ թվերը բաժանվում 11-ի, կապված է 11-ի բաժանելիության հայտանիշի հետ։ Հայտանիշը վերհիշեք ինքնուրույն:

2․ Փաստեր եռանիշ թվերի մասին։
Իսկ դուք գիտե՞ք,  եթե վերցնենք ցանկացած եռանիշ թիվ, օրինակ՝ 372-ը,  հաջորդիվ կրկնեք նույն գրելաձևը ստացված վեցանիշ թիվը 372372 միշտ կբաժանվի  7-ի, 11-ի և 13-ի։ Դեռ ավելին, եթե բաժանենք վեցանիշ թիվըմիաժամանակ բաժանենք 7, 11, 13

372372 ։ 7 ։ 11 ։ 13 = 372, կստանանք սկզբնական եռանիշ թիվը։ Այս հատկությունը  տեղի ունի ցանկացած եռանիշ թվի համար։ Ապացուցյը ինքնուրույն:

3․ Գիտե՞ք, որ եթե վերցնենք 9-ի վրա բաժանվող ցանկացած թիվ և նրա թվանշանները գումարենք, այնքան մինչև ստացվի միանիշ թիվ, ապա ատացված թիվը կլինի՝ 9-ը։ Օրինակ՝ 27513 թիվը 9-ի բաժանվող թիվ է, գումարենք թվանշանները՝ 2+7+5+1+3=18, քանի որ ստացվեց երկնիշ թիվ, էլի գումարենք ՝ 1+8=9։ Ստացվեց 9-ը։

 

7. Խնդիրների թարգմանություն  «Քվանտ»  ամսագրից

1.Արկղում կար 20 մատիտ։ Մաշան ասաց․
-Արկղում կա 5  տարբեր գույնի մատիտներ:
Վիտյան ասաց․
-Արկղում  կա 5 կապույտ և 5 կարմիր մատիտներ։
Եգորն ասաց․
-Դրանցից 10-ը կապույտ են։
Երեխաներից  երկուսը ճիշտ են ասել, իսկ մեկը՝ ոչ։ Ամենաշատը քանի՞ կանաչ մատիտ կարող է լինել  արկղում։

 

 

 

 

 

 

2.  Փղի մեխանիկական ժամացույց-զարթուցիչը փչացել է  և հիմա այն աշխատում է կրկնակի դանդաղ։  Կեսգիշեր է և ժամացույցը ցույց տվեց ճիշտ ժամանակը։ Ամեն անգամ, երգ զնգում է զարթուցիչը, ժամացույցը մի ակնթարթ ցույց է տալիս ճիշտ ժամանակը։ Քանի՞ անգամ կզնգա զարթուցիչը հաջորդ մոտակա երեք օրերին։

 

 

 

 

 

 

3․Գրատախտակին գրված են հետևյալ  թվեր 2, 3, 4, ․․․, ․․․, 29, 30։ Մեկ ռուբլու դիմաց կարելի է ջնջել ցանցած թիվ։ Եթե թիվը ընտրել եք և այն  արդեն ջնջված է, ապա կարող եք  ջնջել նրա բաժանարարները և բազմապատիկները անվճաւ։ Ամենաքիչը քանի՞ ռուբլով կարող ենք ջնջել գրատախտակի բոլոր թվերը։

4․ Հնարավոր է  նշված պատկերը(ուղտը) տրոհել

ա) ցանցի գծերի երկայնքով,

բ) 3 մասի ․(պարտադիր չէ   ցանցի գծերի երկայնքով),  այնպես, որ այդ մասերով հնարավոր լինի ստանալ քառակուսի:

 

Նյութի աղբյուրը այստեղ, էջ՝ 31

Թողարկման պատասխանատուներ.

Սովորողներ՝

• Մարիա Աբրահամյան, Միջին դպրոց, 8-րդ դասարան
• Իռեն Կարապետյան, Միջին դպրոց, 8-րդ դասարան
• Մարիամ Հովհաննիսյան, Ավագ դպրոց, 10-րդ դասարան
• Գուրգեն Մանուկյան Միջին դպրոց, 7-րդ դասարան

Դասավանդողներ՝

• Սյուզի Հակոբյան
• Անի Միրզոյան
• Արշակ Մարտիրոսյան
• Զարինե Փանյան
• Թաթուլ Շահնազարյան

Համարը խմբագրեց Մարի Սարգսյանը՝  Միջին դպրոցի հայոց լեզվի դասավանդողը: