Այս համարում  ներառված են հետևյալ նյութերը.

• Թվային բուրգ
• Մաթեմատիկական խաղ-վիկտորինա
• Տեսողական խաբկանք
• Գիտե՞ս, որ․․․
• Խնդիրներ 5-8-րդ դասարանցիների համար
• Դիրիխլեի սկզբունքը (երկրորդ մաս)
• Խնդիրների թարգմանություն «Քվանտ» ամսագրից

 

 Թվային բուրգ

Սկզբունքը, որով կառուցված է այս թվային բուրգը, պարզ է ու հասկանալի,  հատուկ բացատրությունների կարիք չունի (տե՛ս նկարը): Նայելով նկարին՝  ինքներդ էլ կարող եք հեշտությամբ շարունակել՝ կառուցելով բուրգի մնացած տողերը  դեպի վար, ինչքան որ կամենաք:

Հարց է առաջանում. եթե հետևենք օրինաչափությանը, կպահպանվի՞ արդյոք հավասարությունը թվային  բուրգի մնացած տողերում, միշտ կգտնվի՞  բնական թվի խորանարդ, որ հավասարությունը ճիշտ լինի:

 Մաթեմատիկական խաղ-վիկտորինա

Հյուսիսային դպրոցի դասավանդող Անի Միրզոյանը և ընկերներն առաջարկում են հետևյալ մաթեմատիկական խաղ -վիկտորինան տարատարիք երեխաների համար: Խաղի հարցերը՝  տե՛ս հղումով:

Տեսողական խաբկանք

Հյուսիսային դպրոցի դասավանդող Անի Միրզոյանն առաջարկում է դիտել տեսանյութը և  հարցերին պատասխանել՝  լարելով ուշադրությունը:

Գիտե՞ս, որ…

«Գիտե՞ս, որ…» շարքը առաջարկում է Միջին դպրոցի դասավանդող Լուսինե Ներսեսյանը:

Մեր օրերի առաջին գիրը հասել է շումերներից։ Նշանները հայտնաբերվել են՝ ոսկորների և այլ իրերի մակերեսների  վրա փորագրված: Դրանք, շատերի կարծիքով, թվերի նշաններ են եղել։ Այդ թվանշանները հավանաբար օգտագործվել են անցած ժամանակը հաշվելու, օրերի քանակը, լուսնային ցիկլերը կամ կենդանիների ու այլ օբյեկտների քանակը գրանցելու համար։ Հաշվարկման այս  համակարգերը համարվում են առաջին տեսակի աբստրակտ թվային համակարգեր։
Թվային համակարգի առաջին հայտնի  10 հիմքով համակարգը հանդիպում է մ.թ.ա. 3100-ականների եգիպտական գրություններում։ Դեռ 5000 տարի առաջ Եգիպտոսում արդեն կատարում էին չափումներ, ունեին հստակ թվեր, չափման միավորներ, ճանաչում էին իրենց տարածքի սահմաններն ու կարողանում էին չափել այդ տարածքները: Այդ շրջանում հին եգիպտական թագավորությունն ուներ 8000 քառակուսի մղոն տարածք, իսկ այսօր Եգիպտոսի Արաբական Հանրապետությունը զբաղեցնում է 386660 քառակուսի մղոն տարածք։

Ի՞նչ է մղոնը:
Մղոնը (լատ.՝ mille passuum` «հազար քայլ» բառից)  երկարության չափման միավոր է։ Այն կիրառելի է հիմնականում ծովային հաշվարկներում։ Մղոնի մեծությունը, որ հավասար է միջօրեականի 1՛ աղեղի երկարությանը, տարբեր երկրներում տարբեր է՝ կախված տեղանքի աշխարհագրական լայնությունից և տատանվում է 0, 58 կմ-ից (Եգիպտոս) մինչև 11, 2 կմ (հին չեխական մղոն) սահմաններում։
Հայ մատենագրության մեջ օգտագործված մղոնը 1, 852 կմ է։  Աստվածաշնչում հիշատակվող մղոնը 1479, 5 մ է։
Բազմաթիվ երկրներում կիրառվում է միջազգային ծովային մղոնը, որն ըստ Միջազգային հիդրոգրաֆիական կոնֆերանսի (1929) որոշման՝ հավասար է 1, 852 կմ՝ միջօրեականի 1՛ աղեղի միջին երկարության։

 

 Խնդիրներ 5-8-րդ դասարանցիների համար

1. Մեկ բաժին պաղպապաղակ գնելու համար Պետիային պակասում էր 7 կոպեկ, իսկ Մաշային՝  1 կոպեկ: Նրանք  միավորեցին իրենց ունեցած փողերը: Սակայն դա էլ բավական չէր պաղպաղակ գնելու համար: Ի՞նչ արժեր մեկ  բաժին պաղպաղակը:
2. Ես գնում են գնացքով, որը շարժվում է 40կմ/ժ արագությամբ և տեսնում եմ, թե ինչպես 3 վայրկյանի ընթացքում իմ պատուհանի մոտով անցնում է հանդիպակաց գնացքը, որն ունի 75մ երկարություն: Ի՞նչ արագությամբ էր ընթանում հանդիպակաց գնացքը:
3. Տրամվայի ուղևորը նկատեց իր ծանոթին, որը գնում էր տրամվայի գծի երկայնքով հակառակ ուղղությամբ: 10 վայրկյանից ուղևորը դուրս եկավ տրամվայից և գնաց` իր ծանոթին հասնելու: Որքա՞ն ժամանակից նա կհասնի ծանոթին, եթե շարժվում է իր ծանոթից 2 անգամ արագ, բայց տրամվայից 5 անգամ դանդաղ:
4. Այս խնդրում տառերով ծածկագրված են թվեր: Միանման տառերը նշանակում են միանման թվեր: Փորձեք օրինակը վերծանել.

5. 100 խորանարդներից 80-ն ունեն կարմիր նիստ, 85-ը՝ կապույտ, 75-ը՝ կանաչ: Ինչպիսի՞ն է երեք գույն                 նիստ ունեցող  խորանարդների ամենափոքր թիվը:

6. Արտահայտել մեկ անհավասարությունով. a թիվը մեծ է -1 և փոքր է 1-ից:

7.Չորս մարզուհիներ՝ Անյան, Վալյան, Գալյան և Դաշան, մարմնամարզության մրցմանը գրավեցին առաջին չորս տեղերը, ընդ որում, նրանցից ցանկացած երկուսը  չէր  կիսում ցանկացած երկու տեղ: Հարցին, թե յուրաքանչյուրը որ տեղն է գրավել,  3 հանդիսատես տվեցին տարբեր պատասխաններ.
1) Անյան՝ 2-րդ, Դաշան՝  3-րդ;
2) Անյան՝  1-ին, Վալյան՝ 2-րդ;
3) Գալյան՝  2-րդ, Դաշան՝  4-րդ;
Յուրաքանչյուր պատասխանում մեկ պնդումը ճիշտ է, իսկ մյուսը՝ սխալ: Ո՞ր տեղը զբաղեցրեց յուրաքանչյուր մարզուհին:

8.Գտնել հնգանիշ թիվը, որը 9-ով բազմապատկելուց հետո ցույց է տալիս նույն թիվը, բայց հակառակ դասավորությամբ:

Հղումը տե’ս այստեղ:

 

 Դիրիխլեի սկզբունքը ( երկրորդ մաս)

Դիրիխլեի սկզբունքը և չորս խնդիրների լուծումներ այդ սկզբունքով ներկայացրել ենք «Մաթեմատիկա» ամսագրի 11-րդ համարում (տե´ս  հղումը):

Խնդիր 5։ Միավոր կողմով կանոնավոր եռանկյան ներքին տիրույթում ընտրված են կամայական 5 կետեր։ Ապացուցել, որ այդ կետերի մեջ միշտ կգտնվեն այնպիսի երկուսը, որոնց միջև եղած հեռավորությունը չի գերազանցի 0,5-ը:

Լուծում։ Մինչ  խնդրի լուծումը նկատենք, որ կանոնավոր եռանկյան ներքին տիրույթի կամայական երկու կետերի միջև եղած հեռավորությունը (համաձայն եռանկյան անհավասարության) փոքր է եռանկյան կողմի երկարությունից։ Տրված եռանկյունն իր միջին գծերով բաժանելով 0,5 կողմով չորս կանոնավոր «փոքր» եռանկյունների և վերջիններս դիտարկելով որպես «վանդակներ», իսկ կամայական ձևով ընտրված 5 կետերը՝ որպես «ճագարներ» (թյուր ըմբռնումից խուսափելու համար կպայմանավորվենք միջին գծերին պատկանող կետերն ընդգրկել միայն զուտ միջին գծերով ձևավորված «վանդակ»-եռանկյունում)՝ Դիրիխլեի սկզբունքի համաձայն՝ կարող ենք պնդել, որ կգտնվի 0,5 կողմով այնպիսի կանոնավոր «փոքր» եռանկյուն տիրույթ, որն իր մեջ կպարունակի առնվազն երկու կետ, հետևաբար հենց այդ երկու կետերի միջև եղած հեռավորությունն էլ չի գերազանցի 0,5-ը։

Պնդումն ապացուցված է։

Խնդիր 6։ Միավոր կողով կանոնավոր եռանկյուն բուրգի արտաքին մակերևույթի վրա ընտրված են կամայական 9 կետեր։ Ապացուցել, որ այդ կետերի մեջ միշտ կգտնվեն այնպիսի երկուսը, որոնց միջև եղած հեռավորությունը չի գերազանցի 0,5-ը:

Լուծում: Մինչ խնդրի լուծմանն անցնելը նկատենք, որ կանոնավոր եռանկյուն բուրգի արտաքին մակերևույթի վրա գտնվող կամայական երկու կետերի միջև եղած հեռավորությունը (համաձայն եռանկյան անհավասարության) չի կարող գերազանցել բուրգի կողմնային կողի երկարությանը։ Տրված կանոնավոր բուրգի յուրաքանչյուր նիստ, այն է՝ յուրաքանչյուր կանոնավոր եռանկյուն, իր միջին գծերով բաժանենք չորս հավասար «փոքր» եռանկյունների։ Արդյունքում կունենանք բուրգի յուրաքանչյուր գագաթն ընդգրկող թվով չորս 0,5 երկարությամբ «փոքր» եռանկյունների եռյակներ (որոնց ընդհանուր մակերևույթը պայմանականորեն անվանենք «փոքր» եռանկյուն բուրգերի կողմնային մակերևույթներ), ինչպես նաև բուրգի յուրաքանչյուր նիստին պատկանող և վերջինիս որևէ գագաթ չընդգրկող թվով չորս 0,5 երկարությամբ «փոքր» եռանկյուններ։ Այս՝ թվով 8 տիրույթները դիտարկելով որպես «վանդակներ», իսկ կամայական ձևով ընտրված 9 կետերը՝ որպես «ճագարներ»՝ Դիրիխլեի սկզբունքի համաձայն կարող ենք պնդել, որ կգտնվի մի տիրույթ, այն է՝ «փոքր» եռանկյուն կամ «փոքր» եռանկյուն բուրգի կողմնային մակերևույթ, որն իր մեջ կպարունակի առնվազն երկու կետ, հետևաբար հենց այդ երկու կետերի միջև եղած հեռավորությունն էլ չի գիրազանցի 0,5-ը։ Պնդումն ապացուցված է։

Խնդիր 7։  4×4  չափի քառակուսու ներքին տիրույթում ընտրված են կամայական 15 կետեր (որոնք չեն գտնվում քառակուսու կողմերի վրա)։ Ապացուցել, որ տրված քառակուսու մեջ միշտ կարելի է ընտրել  1×1 չափի միավոր քառակուսի այնպես, որ վերջինիս ներքին տիրույթում որևէ կետ չգտնվի :

Լուծում։ Տրված քառակուսին բաժանելով թվով 16 միավոր քառակուսիների և վերջիններս դիտարկելով որպես «վանդակներ», իսկ կամայական ձևով ընտրված 15 կետերը՝ որպես «ճագարներ», ցանկացած դասավորության դեպքում կունենանք դատարկ «վանդակ», որն էլ կհանդիսանա հենց որոնելի  1x 1 չափի միավոր քառակուսին։
Պնդումն ապացուցված է։

Դիրիխլեի սկզբունքն իր օգտակար և արդյունավետ կիրառությունն ունի նաև բաժանելիության հետ կապված շատ խնդիրներում։ Հաշվի առնելով այն փաստը, որ կամայական բնական թիվ տրված n բնական թվի վրա բաժանելիս առաջացած մնացորդը կարող է ընդունել n հատ հնարավոր արժեքներ, այն է՝ 0; 1; 2; …; n-1, Դիրիխլեի սկզբունքից անմիջականորեն հետևում է հետևյալ կարևոր պնդումը։

Պնդում 1։ Կամայական n +1 հատ բնական թվերի մեջ միշտ կգտնվեն այնպիսի երկուսը, որոնք n-ի վրա բաժանելիս կունենան  նույն մնացորդը (և, հետևաբար, այդ նույն թվերի տարբերությունը կբաժանվի n-ի)։

Խնդիր 8։ Ապացուցել, որ գոյություն ունի միայն 1-երից կազմված բնական թիվ, որը բաժանվում է 1997-ի ։

Լուծում։ Ըստ պնդում 1-ի, բավական է դիտարկել միմյանցից տարբեր, թվով 1998 հատ կամայական բնական թվեր և կարող ենք պնդել, որ նրանց մեջ կգտնվեն այնպիսի երկուսը, որոնց տարբերությունը կբաժանվի 1997 -ի։

Մասնավորաբար, որպես այդպիսիք կարելի է դիտարկել հետևյալ թվերը՝

1; 11; 111;… ; 11… 1(1998 հատ մեկ) ։ Ուստի, ելնելով վերոգրյալից, կարող ենք պնդել, որ գոյություն ունեն m և n բնական թվեր այնպիս, որ

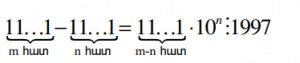
քանի որ (10;1997 ) = 1  ուրեմն

Պնդումն ապացուցված է։

Նկատենք, որ խնդիր 8-ում 1997-ը կարելի է փոխարինել 10-ի հետ փոխադարձաբար պարզ ցանկացած բնական թվով, և դեռ ավելին, նմանատիպ պնդում կարելի է ձևակերպել ոչ միայն միայն 1-երից կազմված թվերի համար, այլ նաև կամայական, միևնույն թվանշանից կազմված բնական թվերի համար։ Ամփոփելով կարող ենք ասել, որ Դիրիխլեի սկզբունքն  իր օգտակար և արդյունավետ կիրառությունն ունի մաթեմատիկայի  դասընթացի տարբեր տիպային և ոչ տիպային խնդիրներում:

Առաջարկում ենք  ևս մեկ խնդիր բաժանելիության վերաբերյալ, որի լուծումը փորձեք գտնել ինքնուրույն։

Խնդիր 9։ Ապացուցել, որ գոյություն ունեն 4 հիմքով և բնական ցուցիչներով երկու այնպիսի աստիճաններ, որոնց տարբերությունը բաժանվում է 2009-ի։

Նյութի աղբյուրը՝ Պետրոսյան Գ., Պետրոսյան Պ., Սովորողների հետաքրքրությունների զարգացումը դիդակտիկական խաղերի օգնությամբ, «Բնագետ», 2012, հ. 4, էջ.102-103:

 

 Խնդիրների թարգմանություն  «Քվանտ» ամսագրից

1․ Հայտնի է, որ (a – b + 2007), (b – c + 2007), (c – a + 2007) թվերը հաջորդական ամբողջ թվեր են։ Գտե´ք  այդ թվերը։

2․ Երկու բնական  թվերի գումարը  2007 է։ Ինչպիսի՞ ամենամեծ արժեք կարող է ընդունել  մեծ թիվը փոքրին բաժանելիս ստացված մնացորդը։

3․ Շախմատի սպիտակ քարերը ( 8 զինվոր, 2 նավակ և այլն) վիճեցին և որոշեցին միմյանց  հարվածել։ Կարո՞ղ է շախմատիստը  սպիտակ քարերը դասավորել  շախմատի տախտակի վրա այնպես, որ ոչ մի քար չկարողանա մյուսին հարվածել։

4․ Մաթեմատիկոս C- ն առաջարկեց հանելուկ A և B մաթեմատիկոսներին.

– Ես մտապահել եմ երեք զույգ տարբեր բնական թվեր, որոնց արտադրյալը չի գերազանցում 50-ը: Ես այդ թվերի արտադրյալը գաղտնի կասեմ  A-ին,  իսկ այդ թվերի  գումարը՝ B – ին: Փորձեք գուշակել այդ թվերը
A-ն և B-ն, համապատասխանաբար իմանալով  թվերի արտադրյալը և թվերի գումարը, սկսեցին հետևյալ  երկխոսությունը.
A —  Ես  այդ թվերը չգիտեմ:
B — Եթե ինձ ասեր թվերի արտադրյալը, ապա ես կիմանայի, որոնք են այդ մտապահած թվերը:
A — Միևնույնն է, ես  չգիտեմ այդ թվերը․
B — Ես էլ չգիտեմ․
A — Իսկ ես արդեն գիտեմ․
B — Ես էլ։
Որո՞նք էին այդ թվերը:

Խնդիրներն տես հղումով, էջ 4

 

Թողարկման պատասխանատուներ.

Թողարկող՝  Մարիա Աբրահամյան, Միջին դպրոց 8-րդ դասարան

Թարգմանեցին՝

Տիգրան Գրիգորյան, Միջին դպրոց 8-րդ դասարան

Գոհարինե, Մարիա Ազնաուրյաններ, Միջին դպրոց 8-րդ դասարան

Իռեն Կարապետյան, Միջին դպրոց 8-րդ դասարան

Դասավանդողներ՝

Լուսինե Ներսեսյան, Միջին դպրոց

Անի Միրզոյան, Հյուսիսային  դպրոց

Խմբագիր՝ Մերի Սարգսյան